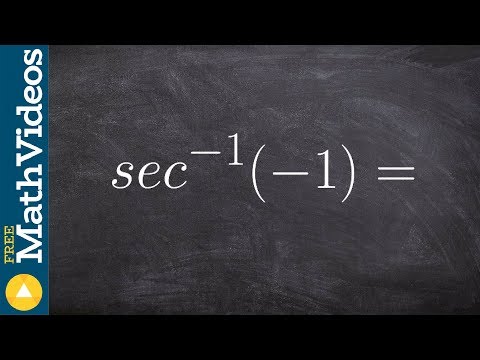
Содержание
- Блок Круг
- Радианы против Градусов
- Степени, минуты и секунды дуги
- Arcsecond: земные и небесные приложения
Круги являются одними из самых фундаментальных форм как в мире природы, так и в технике человека. Звезды, которые являются сферами (или объектами, приближенными к сферам, чтобы быть разборчивыми), способны давать жизнь таким планетам, как Земля. Проекция, или геометрическая тень, сферы - это круг, и обе эти формы имеют бесчисленные значения в астрономии, математике, архитектуре и в других местах.
Блок Круг
Круг можно разделить на 360 градусов или 360 °. То есть одна «поездка» по кругу составляет угол 360 °; альтернативно, 1/360 окружности «захватывается» на один угловой градус.
Каждый градус, как и каждый час на часах, можно разделить на 60, чтобы получить минуты (в данном случае, угловые минуты), а затем снова на 60, чтобы получить секунды. Таким образом, число угловых секунд в круге значительно:
frac {60 ; {arcsec}} {; {arcmin}} × frac {60 ; {arcmin}} {1 ; {°}} × frac {360 ; {градусов }} {; {circle}} = 1 296 000 ; {arcsec / circle}Радианы против Градусов
Еще один способ измерения углов заключается в радиан, Эта единица измерения учитывает тот факт, что окружности и я безнадежно переплетены. Поскольку радиус в 2π равен длине окружности, углы окружности можно измерять в радианах, причем 2π из них составляют один полный оборот.
Поскольку один полный оборот также составляет 360 °, на 360 ° имеется 2π радиан, что составляет 360 / (2 × 3,14159) = 57,3 градуса на радиан. Аналогично, 2π радиан / 360 ° = 0,017453 радиан на градус. Чтобы преобразовать радианы в угловые секунды, умножьте их на 206 265 угловых секунд на радиан.
Выбираете ли вы работать в градусах, радианах или угловых секундах, полностью зависит от параметров и масштаба проблемы, над которой вам предстоит работать.
Степени, минуты и секунды дуги
Если вы смотрите на диаграмму круга на типичном экране телефона или даже на ноутбуке, было бы трудно представить, как будет выглядеть одна полоска этого круга, если бы она была разделена на 360 частей, а тем более 21 600 частей ( общее количество отдельных минут) или более миллиона штук (все секунды).
Но если вы стоите, скажем, на Земле, вокруг которой около 25 000 миль, история изменится. Теперь 25 000 миль / 1 296 000 угловых секунд = 0,0193 мили за угловые секунды. Умножение этого на 60 дает 1,16 миль на дугу в минуту, а умножение снова на 60 дает около 69,4 миль на градус. Фактически, это очень близко к количеству миль в минуту широты в системе координат сетки Земли.
Поскольку линии долготы сходятся (сближаются) между экватором и их встречей на полюсах, эти линии не находятся на фиксированном расстоянии друг от друга, в отличие от линий широты (по этой причине также называемых «параллелями»).
Arcsecond: земные и небесные приложения
Когда вы смотрите на солнце или луну, вы можете подумать, что они занимают большую часть неба, возможно, пару градусов по дуге. Вместо этого каждый диск занимает около 1/2 ° (1800 угловых секунд) неба. Многим людям эта цифра кажется удивительно низкой, возможно, потому, что это самые большие объекты на небе, несмотря на их объективно скромные пропорции. Противоречиво представить, что 360 солнц или лун аккуратно соединяются, чтобы поднять 180 ° неба между горизонтами, но это было бы возможно.
Этот и вышеприведенный раздел иллюстрируют полезность угловых секунд или угловых секунд: очень маленькие фрагменты кругов могут иметь значительные пропорции, если размер круга в целом достаточно велик!