Как рассчитать длину волны серии Бальмера

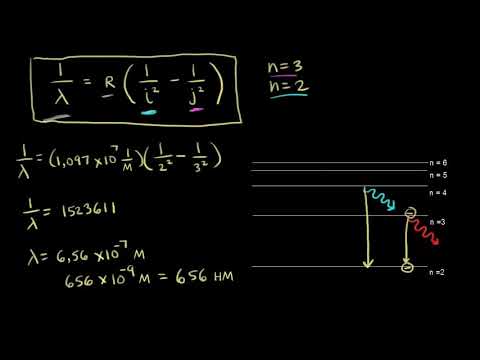
Содержание

• TL; DR (слишком долго; не читал)
• Формула Ридберга и Формула Бальмера
• Вычисление длины волны серии Бальмера

Ряд Бальмера в атоме водорода связывает возможные электронные переходы вплоть до N = 2 положение на длину волны излучения, которое наблюдают ученые. В квантовой физике, когда электроны переходят между различными уровнями энергии вокруг атома (описывается главным квантовым числом, Nони либо выпускают, либо поглощают фотон. Серия Бальмера описывает переходы с более высоких энергетических уровней на второй энергетический уровень и длины волн испускаемых фотонов. Вы можете рассчитать это с помощью формулы Ридберга.

TL; DR (слишком долго; не читал)

Рассчитайте длину волны переходов водородного ряда Бальмера на основе:

1/λ = р_ЧАС ((1/2²) − (1 / N₂²))

где λ это длина волны, р_ЧАС = 1.0968 × 10⁷ м⁻¹ а также N₂ является основным квантовым числом состояния, из которого переходит электрон.

Формула Ридберга и Формула Бальмера

Формула Ридберга связывает длину волны наблюдаемых излучений с основными квантовыми числами, участвующими в переходе:

1/λ = р_ЧАС ((1/N₁²) − (1 / N₂²))

λ символ представляет длину волны, и р_ЧАС является постоянной Ридберга для водорода, с р_ЧАС = 1.0968 × 10⁷ м⁻¹, Вы можете использовать эту формулу для любых переходов, а не только для тех, которые связаны со вторым уровнем энергии.

Серия Balmer просто устанавливает N₁ = 2, что означает значение главного квантового числа (N) два для рассматриваемых переходов. Формула Бальмера поэтому может быть написана:

1/λ = р_ЧАС ((1/2²) − (1 / N₂²))

Вычисление длины волны серии Бальмера

Первый шаг в расчете - найти принципиальное квантовое число для рассматриваемого вами перехода. Это просто означает, что вы ставите числовое значение на «энергетический уровень», который вы рассматриваете. Таким образом, третий уровень энергии имеет N = 3, четвертый имеет N = 4 и так далее. Они идут в месте для N₂ в уравнениях выше.

Начнем с вычисления части уравнения в скобках:

(1/2²) − (1 / N₂²)

Все, что вам нужно, это значение для N₂ Вы нашли в предыдущем разделе. За N₂ = 4, вы получите:

(1/2²) − (1 / N₂²) = (1/2²) − (1 / 4²)

= (1/4) − (1/16)

= 3/16

Умножьте результат из предыдущего раздела на постоянную Ридберга, р_ЧАС = 1.0968 × 10⁷ м⁻¹, чтобы найти значение для 1 /λ, Формула и пример расчета дают:

1/λ = р_ЧАС ((1/2²) − (1 / N₂²))

= 1.0968 × 10⁷ м⁻¹ × 3/16

= 2 056 500 м⁻¹

Найдите длину волны для перехода, разделив 1 на результат из предыдущего раздела. Поскольку формула Ридберга дает обратную длину волны, вам нужно взять обратную величину результата, чтобы найти длину волны.

Итак, продолжаем пример:

λ = 1/2 056 500 м⁻¹

= 4.86 × 10⁻⁷ м

= 486 нм

Это соответствует установленной длине волны, излучаемой в этом переходе на основе экспериментов.