Как рассчитать межплоскостное расстояние

Содержание

• TL; DR (слишком долго; не читал)
• Индексы Миллера
• Константы решетки
• Межплоскостное расстояние для кубической системы и тетрагональных систем

Когда атомы превращаются в решетчатые структуры, как это происходит в металлах, ионных телах и кристаллах, вы можете думать о них как о геометрических фигурах, таких как кубы и тетраэдры. Реальная структура, которую принимает конкретная решетка, зависит от размеров, валентностей и других характеристик атомов, образующих ее. Межплоскостное расстояние, которое представляет собой расстояние между наборами параллельных плоскостей, образованных отдельными ячейками в решетчатой ​​структуре, зависит от радиусов атомов, образующих структуру, а также от формы структуры. Существует семь возможных кристаллических систем, и в каждой системе есть несколько подсистем, что в общей сложности составляет 14 различных структур решетки. Каждая структура имеет свою формулу для расчета межплоскостного расстояния.

TL; DR (слишком долго; не читал)

Рассчитайте межплоскостное расстояние для конкретной структуры решетки, определив индексы Миллера для семейства плоскостей и постоянной решетки.

Индексы Миллера

Разумно говорить о расстоянии между плоскостями, только если они параллельны друг другу. Кристаллографы идентифицируют семейство параллельных плоскостей по показателям Миллера. Чтобы найти их, вы выбираете плоскость из семейства и отмечаете точки пересечения плоскости по осям x, y и z. Перехваты Миллера являются взаимными перехватами. Когда один или несколько перехватов является дробным числом, условием является умножение всех трех индексов на коэффициент, который исключает дробь. Индексы Миллера обычно обозначаются буквами h, k и l. Кристаллографы идентифицируют конкретную плоскость, заключая индексы в круглые скобки (hkl), и показывают семейство плоскостей, заключая их в круглые скобки {hkl}.

Константы решетки

Константа решетки конкретной кристаллической структуры является мерой того, насколько плотно упакованы атомы в структуре. Это зависит от радиуса (r) каждого из атомов в структуре, а также от геометрической конфигурации решетки. Например, постоянная решетки (a) для простой кубической структуры a = 2r. Кубическая структура, включающая атом в центре каждого куба, представляет собой объемно-центрированную кубическую (ОЦК) структуру, а ее постоянная решетки a = 4R / √3. Кубическая структура, включающая атом в центре каждой грани, является гранецентрированной кубикой, а ее постоянная решетки a = 4r / √2. Константы решетки для более сложных форм являются соответственно более сложными.

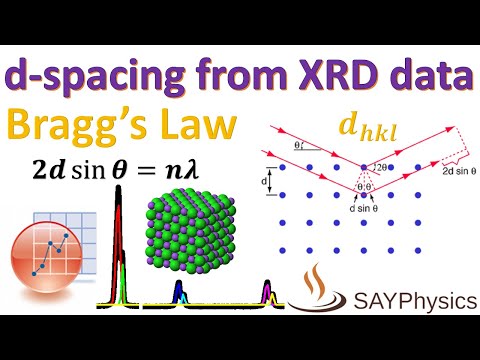
Межплоскостное расстояние для кубической системы и тетрагональных систем

Расстояние между плоскостями в семье с индексами Миллера h, k и l обозначается через d_НЫ, Формула, связывающая это расстояние с индексами Миллера и постоянной решетки (а), существует для каждой кристаллической системы. Уравнение для кубической системы:

(1 / д_НЫ)² = (ч² + к² + л²) ÷ а²

Для других систем взаимосвязь более сложная, потому что вам нужно определить параметры, чтобы изолировать конкретную плоскость. Например, уравнение для тетрагональной системы имеет вид:

(1 / д_НЫ)² = + л²/ с²где с - точка пересечения по оси z.