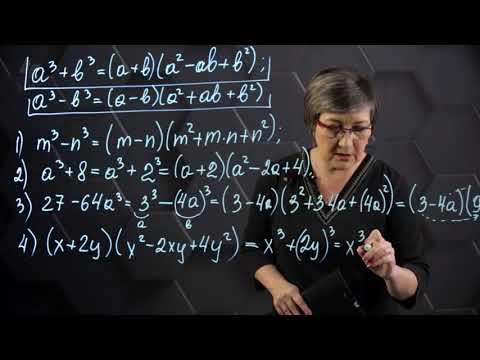
Содержание
Иногда единственный способ пройти через математические вычисления - это грубая сила. Но время от времени вы можете сэкономить много работы, распознавая особые проблемы, для решения которых вы можете использовать стандартизированную формулу. Нахождение суммы кубов и нахождение разности кубов являются двумя примерами именно этого: Как только вы знаете формулы для факторинга 3 + б3 или же 3 - б3найти ответ так же просто, как подставить значения a и b в правильную формулу.
Положить его в жулик
Во-первых, кратко рассмотрим, почему вы можете захотеть найти - или, что более уместно, «фактор» - суммы или разности кубов. Когда концепция впервые вводится, это простая математическая задача сама по себе. Но если вы продолжите изучать математику, позже это станет промежуточным этапом в более сложных вычислениях. Так что если вы получите 3 + б3 или же 3 - б3 в качестве ответа во время других вычислений вы можете использовать навыки, которые вы собираетесь изучить, чтобы разбить эти кубические числа на более простые компоненты, что часто облегчает дальнейшее решение исходной задачи.
Факторинг суммы кубов
Представьте, что вы прибыли в бином Икс3 + 27 и просят упростить это. Первый срок, Икс3, очевидно, это число в кубе. После небольшого осмотра вы можете увидеть, что второе число на самом деле тоже кубическое число: 27 - это то же самое, что и 33, Теперь, когда вы знаете, что оба числа являются кубами, вы можете применить формулу для суммы кубов.
Запишите оба числа в форме куба, если это уже не так. Чтобы продолжить этот пример, вы должны:
Икс3 + 27 = Икс3 + 33
Как только вы привыкнете к процессу, вы можете пропустить этот шаг и сразу перейти к заполнению значений из шага 1 в формуле. Но особенно когда вы учитесь, лучше идти шаг за шагом и напоминать себе о формуле:
3 + б3 = ( + б) (2 - аб + б2)
Сравните левую часть этого уравнения с результатом из шага 1. Обратите внимание, что вы можете заменить Икс на месте а, и 3 вместо б.
Подставьте значения из шага 1 в формулу из шага 2. Итак, у вас есть:
Икс3 + 33 = (Икс + 3) (Икс2 - 3_x_ + 32)
На данный момент прибытие в правую часть уравнения представляет ваш ответ. Это результат деления суммы двух чисел в кубах.
Факторинг Разницы Кубов
Факторизация разности двух чисел в кубах работает одинаково. На самом деле формула практически идентична формуле для суммы кубов. Но есть одно критическое отличие: обратите особое внимание на то, куда идет знак минус.
Представь, что у тебя проблема Y3 - 125 и должны это учитывать. Как прежде, Y3 является очевидным кубом, и, подумав немного, вы сможете понять, что 125 на самом деле 53, Так что у тебя есть:
Y3 - 125 = Y3 - 53
Как и прежде, выпишите формулу для разности кубов. Обратите внимание, что вы можете заменить Y за и 5 для би обратите особое внимание на то, где знак минус идет в этой формуле. Расположение знака минус является единственной разницей между этой формулой и формулой для суммы кубов.
3 - б3 = ( - б)(2 + аб + б2)
Запишите формулу снова, на этот раз подставляя значения из шага 1. Это дает:
Y3 - 53 = (Y - 5)(Y2 + 5_y_ + 52)
Опять же, если все, что вам нужно сделать, это учесть разницу в кубах, это ваш ответ.