
Автокорреляция - это статистический метод, используемый для анализа временных рядов. Цель состоит в том, чтобы измерить корреляцию двух значений в одном наборе данных на разных временных шагах. Хотя данные времени не используются для расчета автокорреляции, ваши приращения времени должны быть равны, чтобы получить значимые результаты. Коэффициент автокорреляции служит двум целям. Он может обнаружить неслучайность в наборе данных. Если значения в наборе данных не являются случайными, то автокорреляция может помочь аналитику выбрать подходящую модель временных рядов.
Вычислите среднее или среднее значение для данных, которые вы анализируете. Среднее значение представляет собой сумму всех значений данных, деленную на количество значений данных (n).
Определите временную задержку (k) для своего расчета. Значение задержки представляет собой целое число, обозначающее, сколько временных шагов отделяет одно значение от другого. Например, задержка между (y1, t1) и (y6, t6) равна пяти, потому что между двумя значениями есть 6 - 1 = 5 временных шагов. При тестировании на случайность вы обычно рассчитываете только один коэффициент автокорреляции, используя лаг k = 1, хотя другие значения лагов также будут работать. Когда вы определяете подходящую модель временного ряда, вам нужно будет рассчитать ряд значений автокорреляции, используя разные значения запаздывания для каждого.
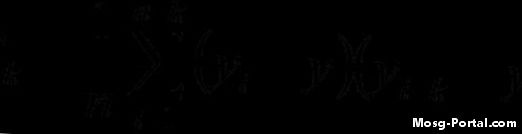
Рассчитать автоковариантную функцию по заданной формуле. Например, если вы рассчитывали третью итерацию (i = 3), используя лаг k = 7, то расчет для этой итерации будет выглядеть следующим образом: (y3 - y-bar) (y10 - y-bar) Итерация по всем значения «я», а затем взять сумму и разделить ее на количество значений в наборе данных.
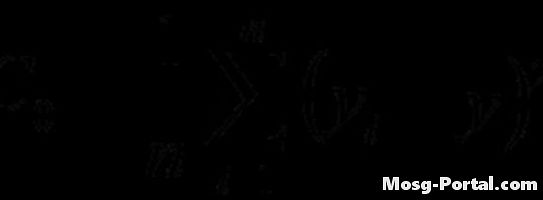
Рассчитать дисперсионную функцию по заданной формуле. Расчет аналогичен функции автоковариации, но запаздывание не используется.

Разделите функцию автоковариации на функцию дисперсии, чтобы получить коэффициент автокорреляции. Вы можете обойти этот шаг, разделив формулы для двух функций, как показано, но во многих случаях вам понадобятся автоковариация и дисперсия для других целей, поэтому целесообразно также рассчитывать их по отдельности.