Содержание
- Механическое преимущество
- Закон сохранения энергии
- Дифференциальный шкив
- Второй закон Ньютона
- Больше висячих блоков
Несколько интересных ситуаций могут быть созданы со шкивами для проверки понимания студентами второго закона движения Ньютона, закона сохранения энергии и определения работы в физике. Одна особенно поучительная ситуация может быть найдена из так называемого дифференциального шкива, распространенного инструмента, используемого в механических цехах для подъема тяжестей.
Механическое преимущество
Как и в случае с рычагом, увеличение расстояния, на которое прикладывается сила, по сравнению с расстоянием, на которое поднимается груз, увеличивает механическое преимущество или рычаги. Предположим, используются два блока шкивов. Один прикрепляется к грузу; один прикрепляется выше к поддержке. Если груз должен подниматься на X единиц, то нижний блок шкивов также должен подниматься на X единиц. Блок шкивов выше не двигается вверх или вниз. Следовательно, расстояние между двумя блоками шкивов должно сокращаться на X единиц. Длина линии, проходящей через петлю между двумя блоками шкивов, должна укорачивать X единиц. Если таких линий Y, то съемник должен тянуть единицы X - Y, чтобы поднять нагрузку единиц X. Таким образом, требуемое усилие в 1 / Y раз превышает вес груза. Говорят, что механическое преимущество Y: 1.
Закон сохранения энергии
Это использование - результат закона сохранения энергии. Напомним, что работа является формой энергии. Под работой мы имеем в виду физическое определение: сила, приложенная к расстоянию нагрузки, на которое нагрузка перемещается силой. Таким образом, если нагрузка равна Z ньютонам, энергия, необходимая для подъема в единицах X, должна равняться работе, выполняемой съемником. Другими словами, Z --- X должен быть равен (сила, приложенная съемником) --- XY. Следовательно, сила, приложенная съемником, равна Z / Y.
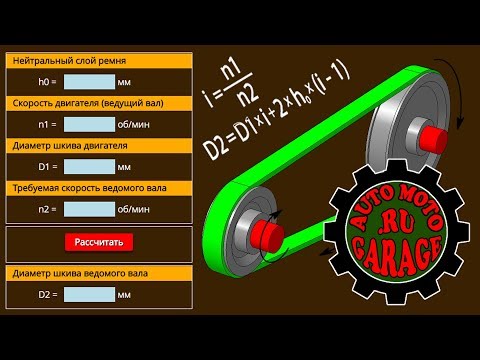
Дифференциальный шкив
Интересное уравнение возникает, когда вы делаете линию непрерывной петлей, и блок, висящий на опоре, имеет два шкива, один немного меньше другого. Предположим также, что два шкива в блоке прикреплены так, что они вращаются вместе. Назовите радиусы шкивов «R» и «r», где R> r.
Если съемник вытягивает достаточно линии, чтобы вращать фиксированные шкивы за один оборот, он вытягивает 2πR линии. Шкив большего размера взял 2πR линии от поддержки нагрузки. Меньший шкив вращался в том же направлении, выпуская 2πr линии к нагрузке. Таким образом, нагрузка возрастает на 2πR-2πr. Механическое преимущество заключается в том, что расстояние вытягивания делится на поднятое расстояние или 2πR / (2πR-2πr) = R / (R-r). Обратите внимание, что если радиусы отличаются только на 2 процента, механическое преимущество составляет колоссальные 50 к 1.
Такой шкив называется дифференциальным шкивом. Это обычное приспособление в автосервисах. Интересным свойством является то, что линия, которую тянет съемник, может свободно висеть, пока груз удерживается на высоте, потому что всегда существует достаточное трение, чтобы противодействующие силы на двух шкивах препятствовали его повороту.
Второй закон Ньютона


Предположим, два блока соединены, и один, называемый M1, свисает со шкива. Как быстро они будут ускоряться? Второй закон Ньютона касается силы и ускорения: F = ma. Масса двух блоков известна (M1 + M2). Ускорение неизвестно. Сила известна по гравитационному притяжению на M1: F = ma = M1 --- g, где g - гравитационное ускорение на поверхности Земли.
Имейте в виду, что M1 и M2 будут ускоряться вместе. Нахождение их ускорения, а, теперь просто вопрос подстановки в формулу F = ma: M1 --- g = (M1 + M2) a. Конечно, если трение между M2 и столом является одной из сил, с которыми F = M1 --- g должна противостоять, то эта сила также легко добавляется в правую часть уравнения, прежде чем ускорение решено за.
Больше висячих блоков

Что делать, если оба блока висят? Тогда левая часть уравнения имеет два слагаемых вместо одного. Более легкий будет двигаться в противоположном направлении от результирующей силы, так как большая масса определяет направление двухмассовой системы; следовательно, гравитационная сила на меньшей массе должна быть вычтена. Предположим, M2> M1. Затем левая часть выше меняется с M1 --- g на M2 --- g-M1 --- g. Правая рука остается прежней: (M1 + M2) a. Ускорение а затем решается тривиально арифметически.