
Содержание
В геометрии восьмиугольник - это многоугольник с восемью сторонами. Правильный восьмиугольник имеет восемь равных сторон и равных углов. Правильный восьмиугольник обычно распознается по знакам остановки. Октаэдр - это восьмигранный многогранник. Правильный октаэдр имеет восемь треугольников с ребрами равной длины. Это фактически две квадратные пирамиды, встречающиеся у их оснований.
Формула восьмиугольника
Формула для площади правильного восьмиугольника со сторонами длины "a" равна 2 (1 + sqrt (2)) a ^ 2, где "sqrt" обозначает квадратный корень.
отвлечение
Восьмиугольник можно рассматривать как 4 прямоугольника, один квадрат в центре и четыре равнобедренных треугольника в углах.
Квадрат имеет площадь ^ 2.
Треугольники имеют стороны a, a / sqrt (2) и a / sqrt (2) по теореме Пифагора. Следовательно, каждый имеет площадь ^ 2/4.
Прямоугольники имеют площадь a * a / sqrt (2).
Сумма этих 9 областей составляет 2a ^ 2 (1 + sqrt (2)).
Объемная формула октаэдра
Формула для объема правильного октаэдра сторон "а" есть ^ 3 * sqrt (2) / 3.
отвлечение
Площадь четырехгранной пирамиды равна площади основания * высоты / 3. Следовательно, площадь правильного восьмиугольника равна 2 * основания * высоты / 3.
База = ^ 2 тривиально.
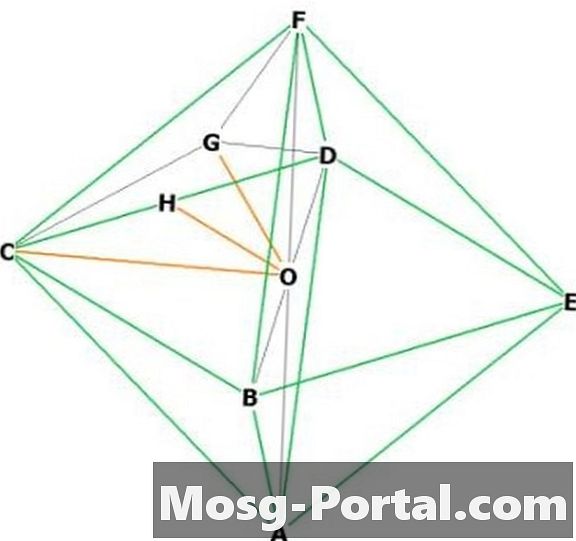
Выберите две смежные вершины, скажем «F» и «C.» «О» находится в центре. FOC - равнобедренный прямоугольный треугольник с основанием "a", поэтому OC и OF имеют длину a / sqrt (2) по теореме Пифагора. Так что высота = а / кв.м (2).
Таким образом, объем правильного октаэдра составляет 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Площадь поверхности
Правильная поверхность октаэдров - это площадь равностороннего треугольника со стороной «а», умноженной на 8 граней.
Чтобы использовать теорему Пифагора, опустите линию от вершины до основания. Это создает два прямоугольных треугольника с гипотенузой длиной «а» и длиной одной стороны «а / 2». Следовательно, третья сторона должна быть sqrt = sqrt (3) a / 2. Таким образом, площадь равностороннего треугольника равна высоте * base / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
С 8 сторон, площадь поверхности правильного октаэдра составляет 2 * sqrt (3) * a ^ 2.