
Содержание
Для того чтобы две формы были конгруэнтными, каждая из них должна иметь одинаковое количество сторон, а их углы также должны быть одинаковыми. Самый простой способ определить, совпадают ли две фигуры, - это повернуть одну из фигур, пока она не будет выровнена с другой, или просто сложить фигуры друг на друга, чтобы увидеть, торчат ли какие-либо концы. Если вы не можете физически перемещать фигуры, вы можете использовать формулы, чтобы определить, совпадают ли фигуры.
Конгруэнтные круги
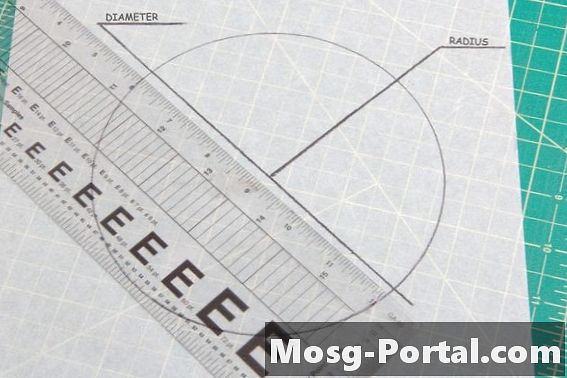
••• Рэй Роберт Грин / Спрос МедиаВсе круги имеют одинаковый угол 360 градусов. Единственным фактором, определяющим конгруэнтность двух окружностей, является сравнение их размера. Диаметр - это прямая линия, проходящая через центр круга от края к краю, а радиус круга - это длина от его центра до его внешнего края. Измерение любого из них на обоих кругах докажет, являются ли они конгруэнтными.
Параллелограммы
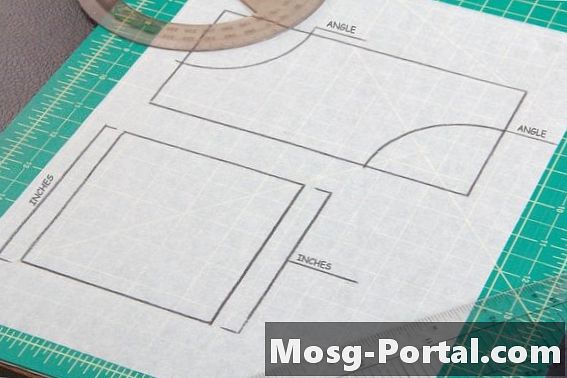
Параллелограмм имеет две пары параллельных сторон, таких как квадраты и прямоугольники. Противоположные стороны или углы параллелограмма имеют одинаковую меру, поэтому необходимо провести два угловых или боковых измерения на параллелограмме, по одному с каждой пары сторон, чтобы сравнить конгруэнтность с другой формой.
треугольники
••• Рэй Роберт Грин / Спрос МедиаЧтобы найти конгруэнтность треугольников, вам нужно определить размер каждого угла или стороны, так как все три могут быть разными. Есть три постулата, которые можно использовать для идентификации конгруэнтных треугольников. Постулат SSS - это когда вы измеряете все три стороны каждого треугольника. Постулат ASA говорит, что если любые два угла и их соединительная сторона совпадают с углом другого треугольника, то они являются конгруэнтными. Постулат SAS делает противоположное, измеряя две стороны и их соединительный угол для сравнения с другим треугольником.
Теоремы для конгруэнтных треугольников

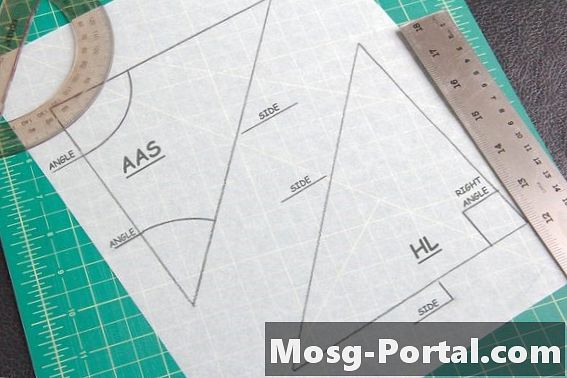
Две теоремы полезны для нахождения конгруэнтных треугольников. Теорема AAS гласит, что если два угла и сторона, не соединяющая два, равны углу другого треугольника, то они совпадают. Теорема о гипотенузе и ноге применима только к треугольникам с одним углом 90 градусов или «прямым» углом. Это когда вы измеряете гипотенузу - сторону, противоположную углу 90 градусов - и одну из других сторон треугольника, чтобы сравнить с другой формой.