Содержание
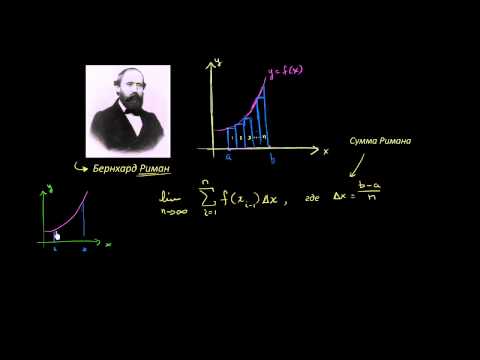
Сумма Римана является приближением площади под математической кривой между двумя значениями X. Эта область аппроксимируется с помощью ряда прямоугольников, которые имеют ширину дельты X, которая выбрана, и высоту, полученную из рассматриваемой функции f (X). Чем меньше дельта X, тем точнее будет приближение. Высота может быть взята из значения f (X) справа, в центре или слева от прямоугольника. Вы можете узнать, как вычислить левую сумму Римана.
Найдите значение f (X) по первому значению X. В качестве примера возьмем функцию f (X) = X ^ 2, и мы аппроксимируем площадь под кривой между 1 и 3 с дельтой X, равной 1; 1 - это первое значение X в этом случае, поэтому f (1) = 1 ^ 2 = 1.
Умножьте высоту, как было найдено в предыдущем шаге, на дельта X. Это даст вам площадь первого прямоугольника. Например, 1 х 1 = 1.
Добавьте дельта X к первому значению X. Это даст вам значение X в левой части второго прямоугольника. Например, 1 + 1 = 2.
Повторите вышеуказанные шаги для второго прямоугольника. Продолжая пример, f (2) = 2 ^ 2 = 4; 4 x 1 = 4. Это площадь второго прямоугольника в примере. Продолжайте в том же духе, пока не достигнете окончательного значения X. Например, есть только два прямоугольника, потому что 2 +1 = 3, что является концом измеряемого диапазона.
Добавьте площадь всех прямоугольников. Это сумма Римана. Завершая пример, 1 + 4 = 5.